Ley inversa del cuadrado de la distancia para la potencia lumínica

Con este pequeño artículo y con el PDF que lo detalla, se pretende ampliar y matizar el enfoque que se da al tema en la obra ELECTROTERAPIA EN FISIOTERAPIA.

Está muy extendido el concepto de que la luz disminuye en su potencia de acuerdo al inverso del cuadrado de la distancia entre el punto de foco y el objeto que la recibe. Importante lo de "punto de foco", ya que se debe considerar el origen de la luz como un punto lo más pequeño posible.

Si se da la circunstancia de que se trabaja con la luz habitual que nos rodea (natural o artificial), como regla muy general, "más o menos" es posible aplicarla.

En fisioterapia se suele tener en cuenta esta reglas en los infrarrojos y en ultravioletas (con lámpara normales), donde se da por bueno que la media de divergencia de los haces luminosos poseen ángulos entre 45º a 55º.

Se explica como sigue (figura 1):

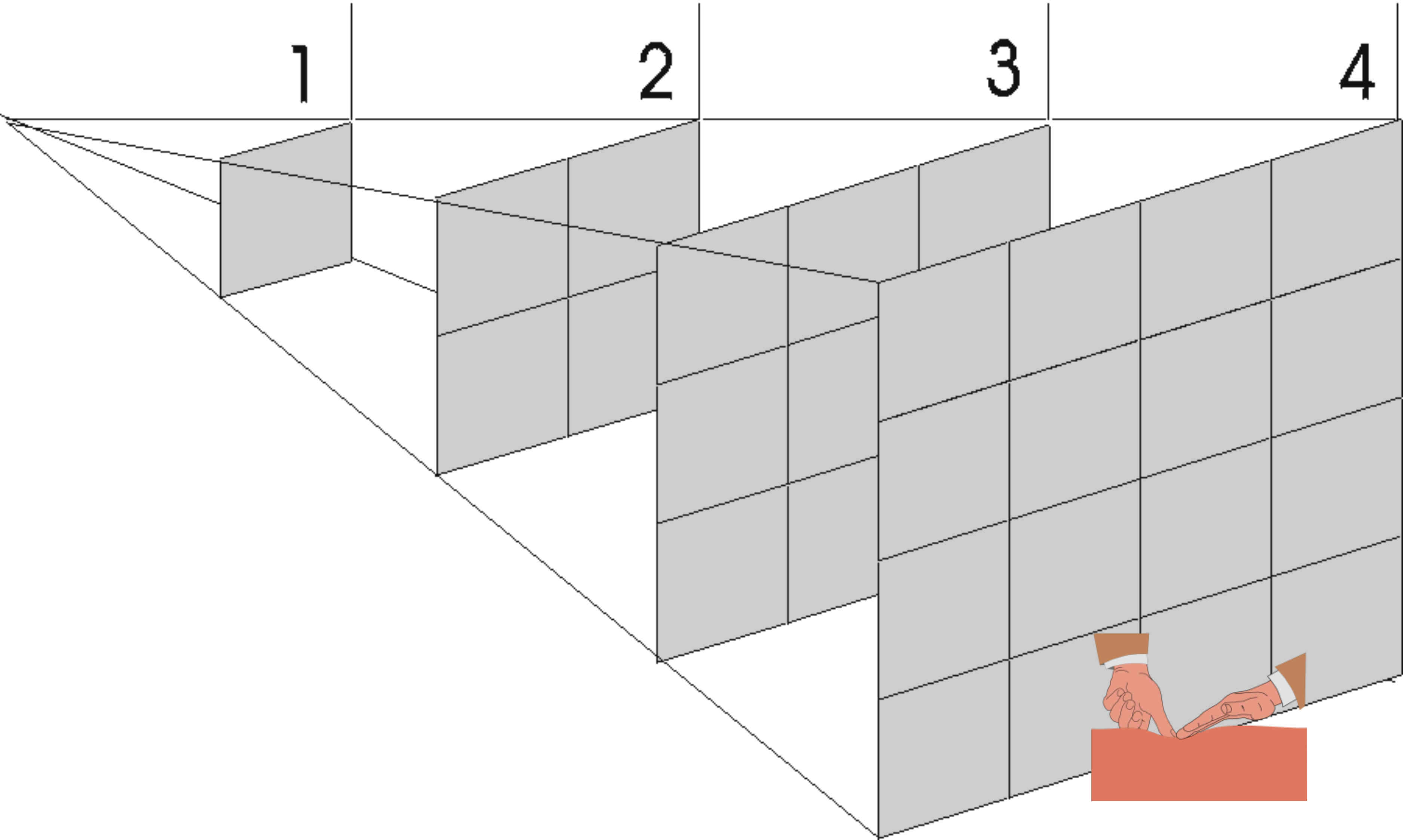
Fig.- 1
Ley inversa del cuadrado de la distancia.

La potencia lumínica recibida en una superficie perpendicular al haz de rayos, cae de forma inversa al cuadrado de la distancia entre el foco y dicha superficie.

Realmente la definición debería ser:

la potencia lumínica recibida en la superficie interna de una esfera es igual a dividir la potencia de origen entre la superficie iluminada, suponiendo que el punto de emisión posee una superficie tendente a cero.

Porque, realmente esto es lo que indica la definición primera. La progresión de la superficie de la esfera es proporcional al cuadrado del radio de la esfera, y en consecuencia, la potencia lumínica disminuye de forma inversa al cuadrado del radio.

El siguiente cuadro lo demuestra:

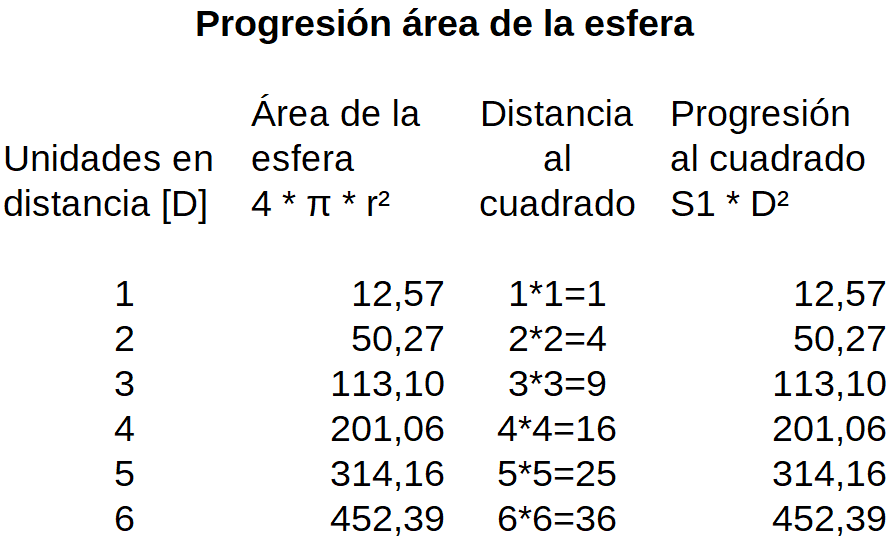
Progresión del área de la esfera de acuerdo con el radio de la esfera [D es el radio de la esfera].

¿Qué ocurre cuando la lámpara no es normal y emite luz con otra divergencia? Pues que esta regla o ley ya no se cumple.

En el siguiente cuadro se muestra la evolución en unidades de superficie y en unidades de distancia (según el gráfico de la "famosa ley" cuadrática inversa) y según la superficie que le corresponde teniendo en cuenta, sobre todo, los grados de divergencia.

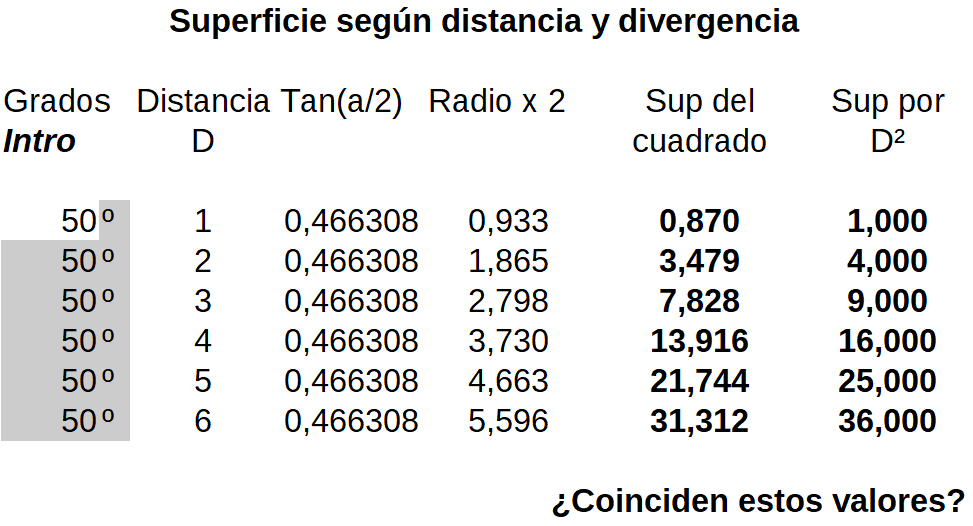
Superficies calculadas según el cuadrado de la distancia y considerando la divergencia del haz.

Si no coinciden los valores de las columnas en negrita, es porque sin  considerar la divergencia, la famosa ley no se cumple. Si se prueban diferentes grados, en los 53.13º se consiguen valores iguales entre ambas columnas. Claro que ese ".13" habría que pasarlo a minutos y a segundos.

Bajarse el archivo y probarlo

Esas superficies se dibujan como cuadrados planos, pero realmente son superficies curvas o porciones esféricas.

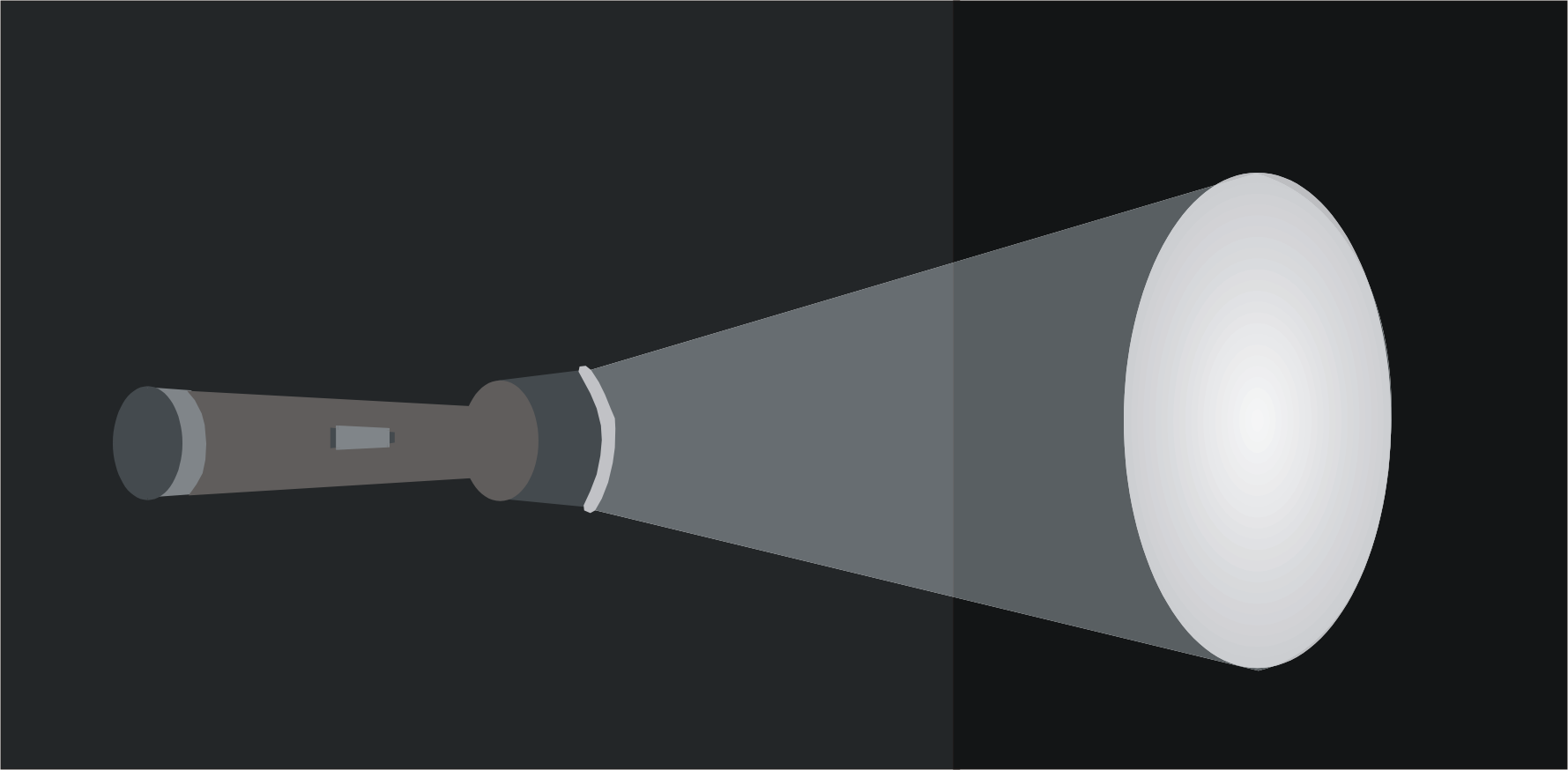
Fig. 2
Luz focalizada con determinado grado de divergencia.

En el láser la divergencia del haz es un parámetro importante a considerar y su divergencia puede tender a ser de 0º, manteniéndose la potencia aunque aumente la distancia. Otro ejemplo que altera esta ley es el simple hecho de hacer converger la luz recibida en la superficie de una lupa, en un pequeño punto (figura 3), con el consiguiente aumento de potencia.

Fig.- 3
Lupa haciendo converger un has de luz hasta provocar fuego por exceso de energía.

Esta ley es aplicable al sol, a las estrellas, a la luz surgida de una explosión, a una bombilla estándar, etc. Pues las lámpara normales de incandescencia emiten luz en todas direcciones y la divergencia de los rayos normalmente se dispersa en los 360º en todos los sentidos (figura 3), hace tiempo era lo que había, pero las variantes de lámparas, focos, diodos, luz focalizada, luz convergente, etc; obliga a considerar que esa ley sea relativa y únicamente se cumple a una divergencia determinada.

Por otra parte, al iluminar zonas planas (o incluso convexas) los bordes reciben menos energía que el centro, dando lugar a la denominada ley del coseno (figura 4).

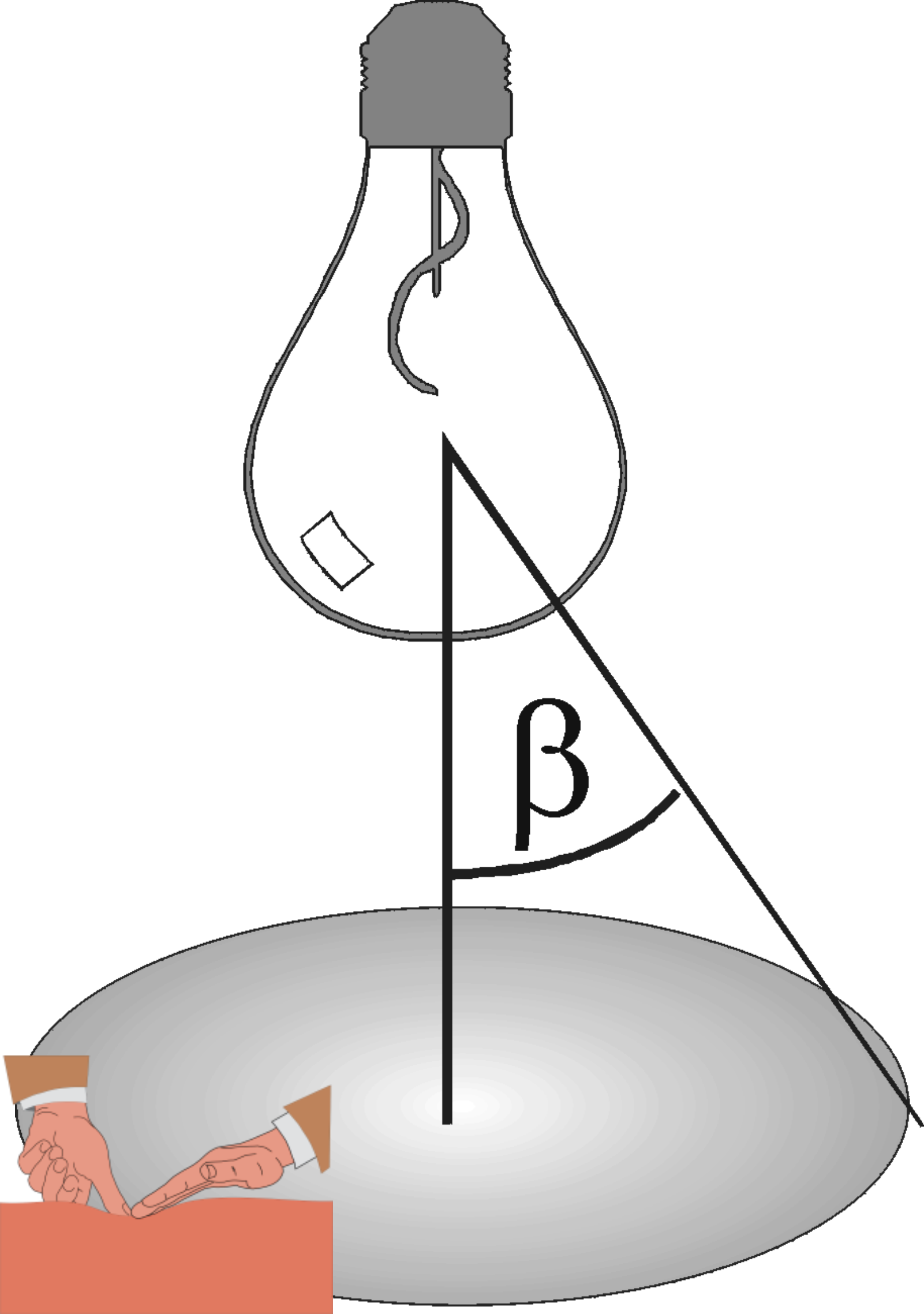
Fig.- 4
Bombilla de incandescencia emitiendo luz en todas las direcciones.

Dada la evolución de las terapias relacionadas con la luz, ya no sirve la simplicidad de la Ley inversa del cuadrado, las circunstancias obligan a establecer una fórmula aplicable a las diversas situaciones que se dan en los tratamientos con infrarrojos, láser, luz focalizada, etc.

Ver el desarrollo del tema en este PDF

Cuando una zona corporal es tratada con una haz divergente (por ejemplo láser) de acuerdo con la distancia, la zona iluminada cambia de tamaño y será muy importante conocer la superficie abarcada para realizar cálculos de la densidad de energía recibida; por ejemplo:

Por supuesto, y con fórmulas simples. Se habla de fórmulas porque la forma de la superficie generada por el haz luminoso puede ser de diferentes formas, tomándose como habituales y más frecuentes la circular y la cuadrada (figuras 4 y 5); simplemente se trata de hallar la superficie de la base de un cono o de una pirámide conociendo la altura y sus ángulos entre la altura (distancia en nuestro caso) y las caras cónicas o laterales. Normalmente dichos ángulos se denominan alfa [α] y beta [β].

El área de la base del cono (figura 4) es simple: superficie es igual a radio al cuadrado por pi

S(cm²) = r² · 3.1416

Aparece una circunstancia que influye en los cálculos, referente a que cuando se habla del grado de divergencia del haz, se refiere a los grados que existen entre los bordes del cono, de manera que la bisectriz de dicho ángulo será la coincidente con la altura o punto central de la base del cono, o de la pirámide en caso del cuadrado. Esto obliga a realizar los cálculos considerando la bisectriz como altura para hallar el radio de la base del cono.

Pero primero hay que conocer el radio partiendo de la altura (distancia) y del ángulo de divergencia (alfa). Así se tiene:

1º.--  ${\displaystyle r=D\cdot tan\left(\frac{\alpha }{2}\right)}$

Que no es lo mismo que:

2º.-- ${\displaystyle r=D\cdot \frac{tan\left(\alpha \right)}{2}}$

En el primer caso se divide el ángulo previamente, mientras que en segundo (no correcta) se divide el resultado de la tangente, siendo valores diferentes.

Según esto, veamos el siguiente caso práctico:

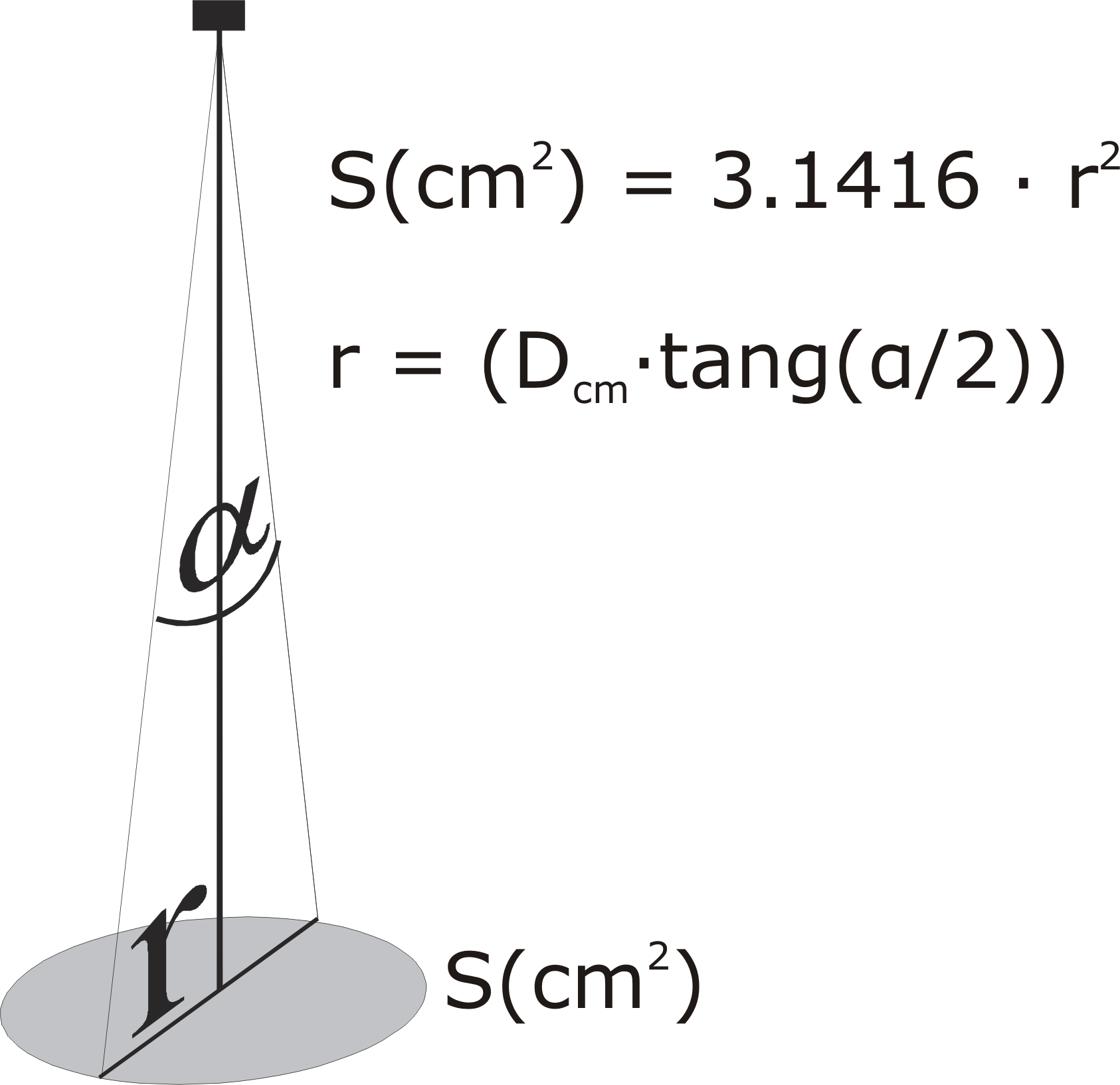
Fig.- 5
Fórmula para calcular la superficie de un haz cónico sabiendo la distancia y el ángulo de divergencia.

Un láser de diodo de 25 W genera un cono circular con una divergencia de 15º ¿Qué superficie de tratamiento generará a 25 cm? ¿Qué potencia recibirá esa superficie?

1º.-- hallar el radio:

Divergencia de 15º entre 2 = 7.5º

tan(7.5º) = 0.131652

Distancia = 25 cm

Radio igual a:

r = 25 · tan(15/2) = 25 · 0.131652 = 3.2913 cm de radio

2º.-- hallar la superficie:

S_cm² = r² · 3.1416 = 3.2913² · 3.1416 = 36.1312 cm² de superficie

En cuanto a la potencia recibida, más adelante se resolverá.

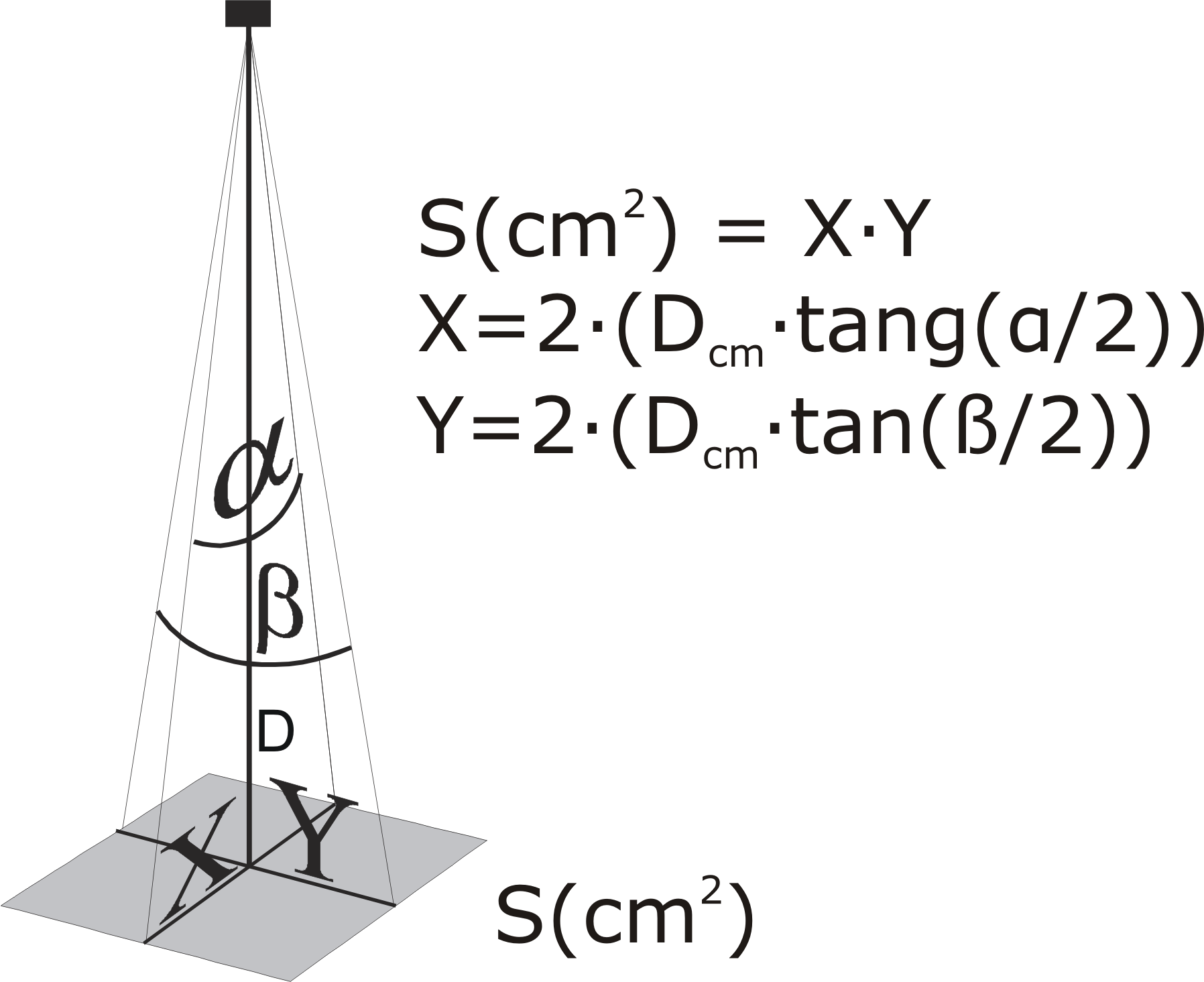
Fig.- 6
Fórmula para calcular la superficie de un haz cuadrado o rectangular sabiendo la distancia y los ángulos de divergencia.

Para el rectángulo es la misma fórmula, salvo que en este caso la superficie se halla multiplicando un lado por el otro [X] e [Y] (equivalente al diámetro en circunferencia), y procede calcular los dos diámetros o lados del cuadrado o rectángulo. (figura 5).

Existe una fórmula para calcular la potencia que llega a la superficie partiendo de la distancia y de la divergencia del haz. Esta es:

Para el círculo:

 _{${\displaystyle W}$${\displaystyle }$${\displaystyle \mathrm{recibida}}$${\displaystyle =\frac{\mathrm{Wemitida}}{D\cdot {tan\left(\frac{\alpha }{2}\right)}^2\cdot 3.1416}}$}

Para el cuadrado:

 _{${\displaystyle \mathrm{Wrecibida}=\frac{\mathrm{Wemitida}}{2\cdot (D\cdot tan\left(\frac{\alpha }{2}\right)\mathrm{·2})}}$}

En esta fórmula, la distancia debe ir en metros.

Retomemos el ejemplo del diodo con haz cónico de 25 W, que decía:

Un láser de diodo de 25 W genera un cono circular con una divergencia de 15º ¿Qué superficie de tratamiento generará a 25 cm? ¿Qué potencia recibirá esa superficie?

La superficie fue resuelta con el valor de 36.1312 cm²

¿Cuál es la potencia recibida?

Potencia emitida = 25 W

Distancia = 0.25 metros

Ángulo divergente / 2 = 7.5º

Tangente de alfa / 2 = 0.131652

Según la fórmula para el círculo:

 _{${\displaystyle W}$${\displaystyle }$${\displaystyle \mathrm{recibida}}$${\displaystyle =\frac{\mathrm{Wemitida}}{D\cdot {tan\left(\frac{\alpha }{2}\right)}^2\cdot 3.1416}}$}

= 25 / 0.25 · 0.131652^2 · 3.1416 = 5.445 W recibidos

5.445 W / 36.1312 cm² = 0.1507 W/cm²

SÍ, PERO NO ES ASÍ

Probas fórmula para el círculo

Probar fórmula para el cuadrado

Quien desee ver a fondo el tema y aclararlo, se sugiere leer este PDF.

Publicado el 21/07/2019